volver

BUCEANDO EN LAS MATEMÁTICAS

aseamos sobre las rocas en una cala de Almería. El mar está tranquilo y transparente, y podemos vislumbrar en su fondo arrecifes de corales y bosques de algas. Atraídos por su belleza y desando ver más, nos metemos en el agua. ¡Qué desilusión! Una vez bajo la superficie, no vemos más que manchas borrosas y sombras. Pero si nos ponemos unas gafas de bucear, entonces nuestros ojos pueden funcionar más allá de sus límites naturales, y el mundo bajo el agua se vuelve nítido y mucho más bello aún de lo que nos parecía desde fuera. Algo parecido ocurre con las matemáticas: o se ven o no se ven, y para verlas se necesitan lentes mentales especiales y entrenamiento en mirar a través de ellas. Pero si son muchos los que, seducidos por las maravillas que se adivinan bajo la superficie de las aguas o por las excelentes fotografías de fondos marinos, se animan a hacerse con unas gafas de bucear, son muy pocos los que tienen la suerte de que un buen maestro o un buen amigo los lleve a la orilla adecuada desde la que poder disfrutar con los tesoros que el océano matemático esconde en sus aguas, y muchos menos los que tiene la ocasión y la paciencia para construirse unas gafas adecuadas con las que bucear entre ellos. Estas son, probablemente, las dos dificultades mayores con las que nos enfrentamos quienes nos dedicamos a la transmisión de las matemáticas. La primera es que, para poder ver los fondos matemáticos, no todas las orillas valen: hay que conocer los lugares desde donde mirar; y la segunda, que nadie vende las gafas adecuadas para sumergirse en ellos; cada cual ha de construirse a medida las suyas propias.

Durante los años de bachillerato, las clases de matemáticas de Pilar Cela dibujaron en mi mente bocetos y formas de hermosas construcciones de álgebra y geometría que me hicieron disfrutar enormemente. Al llegar a la universidad, y sin pensármelo dos veces, me tiré de cabeza en las aguas matemáticas del siglo XX. ¡Menudo chasco me llevé! Pasaba horas en la biblioteca de la facultad intentando descifrar libros y artículos sin ningún éxito; no entendía nada de nada. Me costó tiempo caer en la cuenta de que me había metido en un océano abstracto y que necesitaba hacerme con unas lentes mentales apropiadas si quería ver en él. Aún más tiempo me llevó comprender que las matemáticas del bachillerato me habían entrenado para mirar y pensar llevando puestas como gafas estructuras matemáticas desarrolladas no después del siglo XVIII, y que estas lentes no sólo no me servían ante las matemáticas más recientes, sino que con frecuencia me cegaban (lo mismo, por cierto, les ocurre a los alumnos de hoy). En aquellos años lo que no encontraba en libros se lo preguntaba a mis amigos, y el único amigo a quien interesaron entonces mis preguntas y reflexiones sobre las distintas gafas mentales, José Luis Alexanco, resultó ser pintor. Las conversaciones con José me llevaron, de manera casi automática, a buscar en el arte imágenes con las que ilustrar mis reflexiones y preguntas, y lo que comenzó como búsqueda de un lenguaje común con un amigo se fue convirtiendo con el tiempo en una herramienta valiosa para comprender las estructuras matemáticas contemporáneas. Así, a lo largo de los años y desde mis primeros esfuerzos como estudiante, cuadros, esculturas y piezas artísticas de todo tipo (conceptuales incluidas), me han servido frecuentemente como referencia para ilustrarme a mí misma los nuevos conceptos matemáticos que con que me he ido encarando.

Durante el curso académico 1995-1996, yo debía explicar a un grupo de alumnos de tercero de la Facultad de Matemáticas de la Universidad Complutense de Madrid lo que son las estructuras algebraicas, cómo se construyen, para qué sirven y algunos de los ejemplos más sencillos, como los grupos y los anillos. Llevaba varios meses intentándolo sin éxito y por primera vez desde que empezara a dar clase en la universidad me hallaba totalmente atascada. Claramente, no estaba siendo capaz de transmitir a través de las palabras o la pizarra las imágenes que tenía en la cabeza. Necesitaba encontrar otro punto de vista, otra orilla desde la que señalar a mis alumnos lo que quería que viesen. Durante las vacaciones de Navidad de aquel año fui a visitar a una hermana a Nueva York. Vivíamos en la esquina de West Park Avenue con la calle 94; yo iba caminando todas las mañanas hasta el Museo de Ciencias, en el lado oeste de Central Park, y mientras andaba reflexionaba sobre cómo resolver el evidente problema de comunicación que tenía con mis alumnos de Madrid. Una noche, una tormenta de nieve cayó sobre la ciudad, y al día siguiente el Ayuntamiento canceló todos los autobuses y líneas de metro. Bajé por la calle Amsterdam, fascinada por las luces y las formas. Parecía como si estuviésemos flotando sobre una nube y viviendo en un mundo de ensueño sin líneas rectas; todas las referencias usuales habían desaparecido. Tal era la fascinación que la falta de rectas ejercía sobre mí que me olvidé por completo del Museo de Ciencias y seguí caminando sin prestar atención a la dirección en que lo hacía. En algún momento me encontré frente al Museo de Arte Moderno, y escuché la voz de un hombre que detrás de mí explicaba: "La entrada al museo es gratis hoy debido a la nieve". Entré, y seguí a un grupo de adolescentes, que me llevaron hasta una exposición antológica de Mondrian.

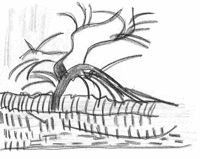
La exposición comenzaba con sus series de árboles. En el primer cuadro, dibujado en 1908 con témpera azul y negra sobre cartón, se reconocía con facilidad uno de esos árboles que se levantan solitarios en mitad de un campo de cultivo. En los últimos, de 1913, sólo aparecían un montón de trazos negros horizontales y verticales, con alguna mancha de color ocre y alguna curva aquí y allá. Quedé como petrificada en mitad de la sala. El proceso que reflejaban los cuadros que tenía ante mis ojos ilustraba con precisión el que yo llevaba meses intentando describir a mis alumnos. Estaba segura de que si pudiese llevarlos hasta allí lo entenderían inmediatamente. Saqué del bolso el cuaderno y los lapiceros y me puse a dibujar los cuadros. Ya que no podía llevar a mis alumnos hasta Mondrian, llevaría a Mondrian hasta mis alumnos (figs. 1, 2, 3).

Mientras dibujaba iba contándome a mí misma, y de paso a unos alumnos imaginarios, lo que estaba viendo: "Mondrian busca hacer abstracción de todo lo que no es la estructura interna del árbol, ignorar las hojas, los colores, la estación del año... Nada de eso aparece descrito en los últimos lienzos, en los que sólo nos muestra el esqueleto de líneas que subyace a un árbol y que describe las relaciones de proporción entre las ramas y su dirección". Con la certidumbre de saberme ante la solución a mi problema, seguí caminando por la exposición. Unas salas más adelante encontré la misma búsqueda del esqueleto en las series sobre fachadas y malecones. Continué hablándome a mí misma: "Siguiendo un proceso en esencia análogo al de los matemáticos en su búsqueda de estructuras, Mondrian sólo presta atención a lo que es permanente; quiere extraer lo que es general, universal, de entre lo que es particular. Entre la confusa multiplicidad de formas que el ojo percibe (en un árbol o una fachada de iglesia, por ejemplo), elige unas cuantas líneas como guía. Este proceso lo lleva gradualmente a la posición extrema de mantener como único contenido formal del cuadro una cuantas líneas verticales y horizontales. Deja detrás cualquier referencia que permita al observador identificar lo que ve con algo que conoce. Busca lo inmutable".

Salí del museo y seguí caminando. Mondrian me serviría para ilustrar en qué consiste la búsqueda de las estructuras que caracterizan a los distintos objetos, pero, ¿cómo hacer ver que son necesarias? Por supuesto, una vez construidas basta con utilizarlas para darse cuenta de su utilidad, pero desarrollar algunas de las estructuras matemáticas que tenía in mente iba a requerir de muchas horas de trabajo por parte de mis alumnos, un trabajo difícil que les resultaría mucho más llevadero si tuviesen alguna idea, por intuitiva que fuese, de qué andaban construyendo.

Mientras daba vueltas en la cabeza a estas cuestiones miraba a mi alrededor. Tras varias horas de sol, la nieve había comenzado a derretirse, y entre las suaves superficies blancas empezaban a emerger, a veces con apariencia de andamios, a veces con aspecto de esqueletos, las esquinas de los edificios. Yo buscaba cómo explicar a mis alumnos la estructura que, formada por rectas, nos ayuda a identificar y estudiar ciertas curvas. De nuevo tenía ante mis ojos una ilustración del proceso. Lo paradójico de la situación me hizo sonreír: gracias a la nieve, la manera de explicarles cómo mirar la estructura que subyace a algunas curvas se me estaba ocurriendo en una ciudad cuyos edificios trazan una línea que combina casi exclusivamente segmentos rectilíneos. Volví a imaginarme ante mis alumnos: "Si intentamos trepar por una, cúpula nos resbalamos. Necesitamos construir un andamio, peldaños en los que apoyar de manera segura los pies. Necesitamos de una estructura que nos sustente".

La búsqueda de estructuras con las que describir y estudiar objetos que en un primer momento nos aparecen como inmanejables es una de las actividades que caracteriza a la matemática el siglo XX. La construcción de estas estructuras requiere lo que llamamos un proceso de abstracción, entendiendo por abstracción distinguir entre lo que es particular (esta cabeza) y lo que es general (cabezas). Si llevamos esta definición a la pintura, serán cuadros abstractos los de Cézanne o Mondrian. Cézanne se encara con una montaña, por ejemplo, y aspira a representar aquello que nos hace reconocer la montaña como tal, independientemente de si la montaña está cubierta de árboles, piedras o nieve, o desnuda. Hace abstracción de lo concreto en la montaña que mira y dibuja la estructura externa, el volumen o contorno que nos permite reconocer el objeto universal "montaña". La estrategia seguida por Mondrian para llevar a cabo el mismo proceso -la identificación de una estructura que permita prescindir de lo concreto en un objeto y quedarnos con lo que es inmutable en él, lo que caracteriza a todos los objetos de su misma naturaleza- es la opuesta. Toma un árbol, por ejemplo, e ignora todo en él salvo las líneas dibujadas por sus ramas, el esqueleto cuyas proporciones y direcciones nos permiten reconocer que estamos ante la estructura interna de un árbol. Cézanne dibuja volúmenes, andamios; Mondrian, esqueletos.

Como en el caso de la pintura, el proceso de abstracción en matemáticas supone la construcción de estructuras asociadas a los objetos concretos, estructuras que nos permiten describir lo universal en estos objetos, eso que es característico no de cada uno de ellos en particular, sino de todos los objetos de su misma especie. Hay muchos tipos de estructuras matemáticas, y en un primer acercamiento, podríamos clasificarlas, como en el caso de la pintura, en dos grupos: externas e internas. Las estructuras externas son andamios que nos permiten percibir un objeto en toda su extensión, de manera que podamos compararlo con otros y decidir "de un vistazo" si son o no de la misma naturaleza. Las estructuras internas son los esqueletos que subyacen y caracterizan a los objetos, y nos permiten identificarlos y aritmetizarlos, es decir, medir en ellos.

Una de las estructuras matemáticas más hermosas es la que se construye a partir de un enlosetado. Se trata de una especie de andamio externo reconocible a primera vista. Pensemos en los cuadros de Cézanne. Es fácil, al mirarlos, darse cuenta de que esas líneas negras, gruesas y discontinuas que hay frente a nosotros representan una montaña. En los cuadros de Cézanne la relación entre las estructuras, los andamios que vemos, y los objetos asociados a ellos es obvia, ya que estas estructuras están basadas en los contornos externos de los objetos, en relaciones que el ojo percibe inmediatamente. Lo mismo ocurre con las estructuras que subyacen a los arabescos de la Alhambra de Granada, por ejemplo. Si observamos sus muros con atención, no tardamos mucho tiempo en reconocer sus simetrías e incluso en poder comparar unas con otras. (Por su parte, las estructuras internas, los esqueletos, no son tan fáciles de reconocer. Ni en matemáticas ni en pintura. Ni es tan fácil entender el proceso de su construcción. Con frecuencia, mantener in mente el proceso seguido por Mondrian en sus cuadros nos ayudará a no perder el hilo de la construcción matemática.)

Todos hemos disfrutado alguna vez con los grabados de M. C. Escher y nos hemos preguntado qué tendría en la cabeza cuando dibujaba aquellas formas. La respuesta es fácil: matemáticas. En 1936 Escher viajó a Granada, y los muros de la Alhambra le causaron una honda impresión. En esa época el artista gráfico holandés intentaba encontrar formas animales con las que recubrir superficies planas, y los arabescos granadinos parecían esconder las claves que buscaba. Un año más tarde descubre el artículo del matemático húngaro George Pólya titulado "Über die Analogie der Krystallsymmetrie der Ebene" ("Sobre la analogía de la simetría cristalina en el plano" [5]. 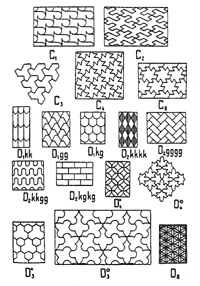En este trabajo, Pólya describe matemáticamente la clasificación de los grupos de simetría bidimensionales y, en concreto, explica con detalle cómo las aparentemente infinitas maneras de recubrir una superficie plana con losetas en forma de paralelogramo se reducen esencialmente a 17, dando ejemplos gráficos de cada una de ellas (fig. 4). En el trabajo de Pólya, Escher encontró la clave que buscaba para entender los muros de la Alhambra -que ofrecen un catálogo completo de las 17 posibilidades-, lo que le permitió desarrollar sus propias reglas para construir simetrías planas y realizar los impresionantes grabados que todos conocemos (Escher recogió sus reglas en un enorme cuaderno que tituló "División regular de un plano con polígonos asimétricos regulares").

Reflexionemos un poquito sobre el trabajo de Pólya. La manera más fácil de recubrir una superficie plana con un diseño es elegir un dibujo inicial en forma de paralelogramo y repetirlo de alguna manera sistemática por toda ella. Los alicatados que suelen ponerse en las paredes de cuartos de baño y cocinas, por ejemplo, tienen por lo general una trama muy sencilla: existe una loseta inicial en forma de paralelogramo que se ha trasladado en todas las direcciones posibles hasta recubrir por completo la pared. Esta trama, esta estructura construida a base de trasladar en todas las direcciones un paralelogramo inicial, supone la manera más fácil de cubrir toda una pared a partir de una loseta inicial. Pero no es la única. Podríamos hacer girar repetidamente el paralelogramo inicial sobre uno de sus ángulos y obtener un diseño estrellado, o reflejarlo en un espejo imaginario y obtener su imagen especular.

Si quisiésemos dar a alguien instrucciones precisas para cubrir toda una pared a partir de un paralelogramo, sólo tendríamos que dar a esta persona dos cosas (llamadas, juntas, la estructura del recubrimiento): una loseta inicial en forma de paralelogramo, con su dibujo, y las transformaciones a las que se ha de someter este paralelogramo inicial para cubrir con él la pared.

Distintas transformaciones de la loseta inicial dan lugar a distintos recubrimientos de una pared. El dibujo que haya dentro de la loseta inicial es anecdótico y resulta irrelevante cuando se trata de resolver el problema de la clasificación de los recubrimientos de una superficie plana. En matemáticas interesa especialmente estudiar aquellos recubrimientos que se obtienen a partir de un paralelogramo inicial sometido tan solo a traslaciones (desplazamientos en una dirección fija), giros y reflexiones (imágenes especulares), es decir, a transformaciones que no lo cambian de tamaño. La razón es que las estructuras así obtenidas, que llamaremos enlosetados por razones obvias, son la versión bidimensional de las estructuras (tridimensionales) que se encuentran en la mayoría de los cristales en la naturaleza.

La primera pregunta a la que hay que responder es, naturalmente: ¿de cuántas maneras distintas podemos enlosetar una pared? Para poder estudiarlo hay que empezar por distinguir entre un enlosetado y otro, y luego contar cuántos hay. Dos enlosetados se consideran distintos si se han obtenido sometiendo las losetas iniciales de cada uno de ellos a transformaciones distintas, y se consideran esencialmente el mismo enlosetado si se han obtenido sometiendo la loseta inicial de cada uno de ellos a idénticas transformaciones. Si queremos comparar dos recubrimientos hechos por nosotros mismos, es fácil saber si son distintos o no, pues conocemos las transformaciones que hemos llevado a cabo con la loseta inicial de cada uno de ellos. Sin embargo, cuando se trata de comparar enlosetados construidos por otros necesitamos poder identificar a qué transformaciones han sido sometidas las losetas iniciales de cada uno de ellos. Estas transformaciones se identifican a través de las simetrías del enlosetado.

En matemáticas llamamos simetrías de un objeto a los movimientos de este objeto que no lo alteran en tamaño ni forma. Pensemos en un enlosetado cualquiera. Hay un dibujo inicial dentro de un paralelogramo que se ha ido reproduciendo sobre la superficie. De esta manera, cualquiera de los trazos o puntos del dibujo inicial vuelve a aparecer muchas veces en el enlosetado. Tantas como veces se haya vuelto a copiar el dibujo y el paralelogramo inicial para obtener el enlosetado. Las simetrías del enlosetado se obtienen de la siguiente manera: primero calcamos el enlosetado sobre papel transparente imaginario, y luego vamos desplazando esta reproducción sobre el dibujo inicial intentando hacer casar las distintas copias del paralelogramo inicial. Un papel puede moverse esencialmente de tres maneras sobre una superficie: puede ser trasladado en una dirección constante, puede ser girado, o se le puede dar la vuelta. No hay más posibilidades. Para identificar las simetrías de nuestro enlosetado no tenemos más que buscar entre estos tres movimientos- traslaciones, giros y reflexiones- aquellos que permiten desplazar la reproducción transparente imaginaria sobre la superficie del enlosetado original de tal manera que los dibujos en ambos sigan encajando uno con otro. A estos movimientos los llamamos las simetrías del enlosetado, y la expresión que se suele utilizar en matemáticas para describir este "proceso mental" de desplazar una copia transparente imaginaria sobre la superficie de un enlosetado de tal forma que los diseños encajen es el de "hacer actuar una simetría". Hacer actuar un giro sobre un enslosetado, por ejemplo, consiste en imaginamos una copia transparente del enlosetado que se despega, como si de una piel se tratase, gira y vuelve a encajarse en el enlosetado como si nada hubiese pasado.

Las simetrías del enlosetado se corresponden exactamente con las transformaciones del paralelogramo inicial que han dado lugar al enlosetado. Si para obtener el enlosetado la loseta inicial fue sometida a una traslación, esta traslación aparecerá entre las simetrías del enlosetado; si se giró la loseta tantos grados en tal dirección, tendrá un giro de tantos grados y en tal dirección como simetría; y, finalmente, si se la reflejó con respecto a un eje imaginario, la reflexión respecto a ese eje aparecerá entre sus simetrías. Cada transformación de la loseta inicial da lugar a una simetría del enlosetado, y cada simetría del enlosetado viene de una transformación de la loseta inicial. A efectos prácticos, esta correspondencia entre transformaciones y simetrías nos dice que para describir la estructura de un enlosetado (las transformaciones que se han de llevar a cabo en la loseta básica para obtener el enlosetado) basta con describir sus simetrías. Hagámoslo.

Un hecho fácil de comprobar es que si hacemos actuar sucesivamente dos simetrías de un enlosetado, obtenemos una tercera simetría de él. Por ejemplo, si llevamos a cabo primero una traslación de dirección horizontal que sea simetría de un enlosetado, y a continuación otra de dirección vertical que también sea una simetría del enlosetado, obtenemos una traslación de dirección diagonal, también simetría del enlosetado.

En general, la regla de "actuación sucesiva" nos permite combinar las simetrías de un enlosetado Esta regla de combinación tiene las siguientes propiedades:

i. Si combinamos dos simetrías de un enlosetado haciendo actuar primero una y luego otra sobre él, producimos una tercera simetría de enlosetado. Por ejemplo, una traslación horizontal, seguida de una vertical, dan lugar a una traslación diagonal.

ii. Dada cualquier simetría de un enlosetado, el movimiento que la "deshace" resulta ser siempre otra simetría del enlosetado. Por ejemplo, el movimiento que deshace un giro de noventa grados alrededor de un punto en la dirección de las agujas del reloj, es el giro de noventa grados alrededor de ese mismo punto y en dirección contraria a lasa de las agujas del reloj.

iii. Si tenemos tres simetrías cualesquiera de un enlosetado, no importa si hacemos actuar primero la primera y a continuación la simetría que se obtiene al combinar la segunda con la tercera, o si primero combinamos las dos primeras y a continuación hacemos actuar la tercera, pues el efecto sobre el enlosetado será el mismo.

iv. Finalmente, si tenemos dos simetrías de un enlosetado, da lo mismo el orden en que las hagamos actuar una después de la otra,

Son muy, muy frecuentes en matemáticas las estructuras que consisten en un conjunto de objetos y una regla para combinar sus elementos i-iv. Tan frecuentes que tienen nombre propio: grupos conmutativos. Dicho con otras palabras, siempre que nos encontremos ante un conjunto de elementos y una regla de combinación de sus elementos que verifique las propiedades i-iv diremos que estamos ante un grupo conmutativo, o bien que el conjunto y su regla de combinación forman (tienen) una estructura de grupo conmutativo. Así pues, el conjunto de las simetrías de un enlosetado junto con la regla de combinación de "actuación sucesiva" forman una estructura de grupo conmutativo conocida como grupo de simetrías del enlosetado.

Repasemos lo que hemos visto hasta ahora. La propiedad que caracteriza un enlosetado es la cantidad de simetrías que tiene, y esta información está codificada en la estructura asociada al enlosetado que acabamos de denominar su grupo de simetrías: los movimientos, combinados unos con otros, que dejan el dibujo del enlosetado invariante. Una vez que hemos identificado las simetrías de un enlosetado, tenemos totalmente identificado de qué tipo de enlosetado se trata, cómo ha sido construido exactamente, y cómo distinguirlo de otros enlosetados. La estructura dibujada por Cézanne para describir una montaña es compartida por todas las montañas del mismo tipo (mismo material, misma zona geográfica, misma forma, etc.). Análogamente, esta estructura que llamamos grupo de simetrías no está asociada tan solo a un enlosetado, sino a toda la familia de enlosetados que se obtienen llevando a cabo las mismas transformaciones de una loseta inicial. Es una estructura que nos permite, al verla, reconocer el tipo de enlosetado ante el que estamos. Las estructuras de Cézanne nos permiten decir "mujer y gorda", "montaña y rocosa", etc.; los grupos de simetrías nos permiten hacer una caracterización similar de los enlosetados del plano. Si el grupo de simetrías de dos de ellos coincide, esto significa que han sido construidos de la misma manera, y por lo tanto son, conceptualmente hablando, el mismo tipo de objeto, el mismo tipo de enlosetado.

Cuando, como en los ejemplos de los muros de la Alhambra o en los alicatados de una cocina, el enlosetado se ha obtenido a partir de una loseta básica, en forma de paralelogramo, sometida a distintas transformaciones, su grupo de simetrías contiene siempre traslaciones, y en tal caso nos encontramos ante un conjunto de simetrías con una estructura muy particular y muy frecuente en la naturaleza. A estas estructuras se las conoce como grupos cristalográficos planos, pues su versión tridimensional es la que encontramos como estructura en casi todos los cristales. Los grupos cristalográficos planos, esto es, los grupos de simetrías de los enlosetados obtenidos a partir de un paralelogramo inicial, son importantes en el estudio de la naturaleza. Por ejemplo, saber cuántos grupos cristalográficos planos existen permite clasificar muchas de las estructuras cristalinas que existen. Después de siglos de trabajo de miles de personas, los matemáticos Pólya y Nigli demostraron en 1924 que hay, como hemos señalado, exactamente 17 de estos grupos; dicho de otra manera, hay exactamente 17 maneras distintas de recubrir una superficie plana a partir de un paralelogramo inicial.

Este tipo de recubrimientos se encuentran en todo el planeta: en diseños de telas y papeles, en relieves de madera, en decoraciones de paredes, etc. De los muchísimos ejemplos del uso de los enlosetados para decorar que podemos encontrar, hay uno que destaca como joya única: el de los arabescos del palacio de la Alhambra. Lo que hace tan especiales a los mosaicos de los muros y celosías de la Alhambra es que contienen ejemplos de las 17 maneras posibles de enlosetar un plano. Esto es, las paredes de la Alhambra nos ofrecen un catálogo completo de los posibles grupos cristalográficos planos, de hecho, el primero construido antes del siglo XX. La Alhambra demuestra, pues, que los árabes habían encontrado las 17 maneras de construir enlosetados antes del siglo XIII. Sin embargo, se ha necesitado muchísimo tiempo, muchas matemáticas y un profundísimo proceso de abstracción para demostrar que estas 17 maneras son, de hecho, las únicas posibles.

Esta búsqueda de las estructuras que subyacen o sirven de andamio a los distintos fenómenos no es exclusiva de las matemáticas o la pintura, sino que de hecho caracteriza mucha de la actividad intelectual del siglo XX. Veamos algunos ejemplos, todos ellos relacionados en mayor o menor grado con las matemáticas.

En diciembre de 1977, el catedrático de Antropología social del Collège de France, Claude Lévi-Strauss, dio en la cadena CBC Radio de la Universidad de Toronto, bajo el título "Myth and Meaning", una serie de conferencias radiofónicas, publicadas posteriormente en forma de libro [3]. En ellas explicaba con ejemplos concretos las estructuras subyacentes a varios de los mitos de los nativos canadienses. La posibilidad planteada por Lévi-Strauss en este y otros trabajos de que el pensamiento sea estructural supuso una manera nueva de colocarse ante los mitos, cuentos y leyendas, una manera que nos permite entender cómo la tradición oral ha contribuido y aún contribuye a estructurar nuestros razonamientos cotidianos, esos razonamientos que, pulidos, dar lugar a las matemáticas. En los orígenes de los trabajos de Lévi-Strauss en esta dirección, se encuentra su colaboración con el matemático André Weil [7]. Cuando Lévi-Strauss y Weil se conocieron en Nueva York, en 1943, el primero llevaba tiempo analizando, sin llegar a entenderlas, las reglas con las que algunas tribus primitivas -i. e., sin escritura- decidían sus matrimonios. Al conocer a Weil, le mostró los datos que había acumulado y éste, utilizando las matemáticas, identificó la estructura subyacente a aquellos enlaces matrimoniales, que resultó ser un grupo conmutativo [8], comentarios a 1949a).

En las sociedades estudiadas por Lévi-Strauss, todos los individuos, hombres y mujeres, están repartidos en clases, y la clase a la que pertenece cada individuo está determinada, según ciertas reglas fijas, por la clase a la que pertenecen sus progenitores. Las reglas matrimoniales indican, según la clase a la que pertenecen un hombre y una mujer, si el matrimonio entre ellos es posible o no. En tales sociedades ocurre además que la totalidad de los matrimonios posibles se pueden repartir en varios tipos; si, y es el caso más sencillo, el número de tipos posibles de matrimonios coincide con el número de clases en las que están repartidos los individuos de la sociedad, hay una fórmula única que, para un individuo de una clase dada, nos indica en qué clase puede elegir pareja con la que casarse. Si el número de tipos de matrimonios es mayor que el número de clases en las que está repartida la sociedad, las posibilidades de elección son mayores, y la traducción al lenguaje algebraico un poco más complicada. Veamos un ejemplo del caso más sencillo. Supongamos que en una sociedad mujeres y hombres están repartidos en cuatro clases A, B, C y D, y que la clase a la que pertenece cada individuo está determinada por la clase a la que pertenece su madre de la manera siguiente: las criaturas de una madre de la clase A, B, C, D pertenecen, respectivamente, a las clases B, C, D, A. Supongamos, también, que en tal sociedad hay cuatro tipos de matrimonios posibles, que denotaremos por M1, M2, M3 y M4, y que son los siguientes: M1, hombre clase A con mujer clase B; M2, hombre clase B con mujer clase C; M3, hombre de clase C con mujer de clase D; M4, hombre de clase D con mujer de clase A.

La regla matrimonial que acabamos de describir satisface dos condiciones:
i) cada individuo tiene derecho a elegir pareja en un único tipo de matrimonio;
ii) el tipo de matrimonio en el que puede elegir un individuo depende exclusivamente de su sexo y del tipo de matrimonio en el que nació.

Así pues, el tipo único de matrimonio que puede elegir una hija fruto de un matrimonio de tipo M1, M2, M3 o M4, depende de (es una función de, diríamos en matemáticas) M1, M2, M3 o M4, respectivamente, y siguiendo la notación matemática, lo denotamos por f(M1), f(M2), f(M3) y f(M4); análogamente, el tipo de matrimonio que puede contraer un hijo de una pareja de tipo M1, M2, M3 o M4 es una función de M1, M2, M3 o M4 que denotamos por g(M1), g(M2), g(M3) y g(M4). Con esta notación, la tabla de matrimonios posibles en esta sociedad es la siguiente:

Al mirar esta tabla nos damos cuenta de que todos los tipos de matrimonios aparecen en todas las generaciones, ninguno se pierde. En el lenguaje matemático esto se expresa diciendo que las funciones f y g son permutaciones -reordenamientos- de M1, M2, M3 y M4. Para hallar los matrimonios posibles a lo largo de una cadena de generaciones, no tenemos más que ir haciendo actuar sucesivamente las permutaciones f y g.

Las permutaciones, introducidas por Lagrange y Galois en el siglo XIX, están completamente clasificadas en matemáticas. El conjunto formado por todas las permutaciones posibles de un número determinado n de elementos (en nuestro caso n=4) con la regla de actuación sucesiva tiene exactamente las mismas propiedades i), ii), ii) y iv) que nos aparecieron al estudiar el conjunto de las simetrías de un enlosetado; se trata, pues, de una estructura de grupo. Los grupos de permutaciones de cuatro elementos están completamente clasificados, y esto nos permite, según las condiciones que verifiquen nuestras reglas de matrimonio, entenderlas e identificarlas. Por ejemplo, supongamos que en nuestra hipotética sociedad exigimos que todo hombre pueda casarse con la hija del hermano de su madre; si reflexionamos un poco sobre ello caemos en la cuenta de que esta exigencia traduce al lenguaje de las permutaciones en la condición:

f(g(M1)=g(f(M1); f(g(M2)=g(f(M2); f(g(M3)=g(f(M3); f(g(M4)=M4.

Sólo hay dos tipos de grupos de permutaciones de cuatro elementos que verifiquen todas las condiciones que verifica el grupo obtenido a partir de las permutaciones f y g de nuestro caso, lo que nos permite clasificar con gran facilidad ante qué tipo de sociedad nos encontramos. Este ejemplo (y cualquier otro de los descritos por Weil en [8]), ilustra la manera en que las reglas matrimoniales de ciertos tipos pueden ser descritas mediante cálculos algebraicos, y cómo el álgebra y la teoría de los grupos de permutaciones pueden facilitar el estudio y clasificación de fenómenos de la vida cotidiana.

En 1917 Marchel Duchamp presentó en Nueva York, en el Armory Show, el primero de su llamados ready-mades, un orinal de porcelana que tituló Fuente. La pieza de Duchamp causó revuelo y escándalo en la comunidad artística, y muchos se preguntaron -y se siguen preguntando- qué tendría Duchamp en la cabeza al elegir semejante objeto como obra. Parece ser que matemáticas [2]. La escultora Rhonda Roland Shearer [6] y su marido, el biólogo Stephen Jay Gould, llevan años recogiendo datos que parecen indicar que los ready-mades de Duchamp y su obra más conocida, El gran vidrio, están inspirados en el ensayo La invención matemática, escrito por el matemático francés Henri Poincaré en 1908 [4]. A lo largo de su vida, Poincaré escribió varios libros de divulgación sobre matemáticas y ciencia. La invención matemática es una reflexión sobre la naturaleza de la creatividad en matemáticas y la manera en la que los "descubrimientos" matemáticos tienen lugar. No cabe duda de que Duchamp trabajó mucho este texto de Poincaré, del que tomó un montón de anotaciones que guardó en la Caja Verde que acompaña a El gran vidrio [2]. Para describir el tipo de matemáticas que el inconsciente produce, Poincaré forja la expresión ready-made, que aparece traducida en la versión castellana primero como todo hecho (pág. 53, l. 3) y, más adelante, como hecho (pág. 53, l. 9)

Pablo Picasso estaba fascinado por los descubrimientos de las geometrías no euclídeas y en cuatro dimensiones llevados a cabo por los matemáticos del siglo XIX. La influencia que estos trabajos tuvieron en sus cuadros está muy bien documentada [1]. No es de sorprender que Picasso prestase atención a las estructuras geométricas matemáticas. Supongamos que tenemos delante de nosotros la cara de una persona de la que queremos dar una descripción lo más completa posible. Lo primero que hacemos es movernos en derredor suyo y observarla desde todos los ángulos posibles. Cuando fijamos la atención en su ojo izquierdo, el derecho nos aparecerá borroso. Para ver el segundo ojo, habremos de variar la dirección de nuestra mirada, y entonces será el ojo izquierdo el que veamos borroso. Y tampoco podremos disfrutar simultáneamente del perfil de su nariz y la palma de una de sus manos. Para poder ver la figura en su totalidad habremos de movernos, y al hacerlo obtendremos diversas imágenes parciales. Son estas imágenes parciales lo que llamamos datos locales. Reconstruir a continuación la figura como un todo único a partir de estos datos locales, dar lo que llamamos una descripción global del objeto de nuestro estudio, plantea de inmediato dos problemas. El primero, seleccionar de entre todos los datos locales un número suficiente, pero ciertamente finito, con los que trabajar. El segundo, cómo encolar de manera coherente en una imagen global única diversos datos locales. A lo largo del siglo XX, y equipados con las herramientas y estructuras desarrolladas en la época de Cézanne y Mondrian, pintores y matemáticos se enfrentaron a la tarea de dar una descripción global de un objeto a través de varias descripciones locales. El problema, tanto para los matemáticos como para los pintores, fue, es, cómo encolar las distintas descripciones locales de manera coherente y producir a partir de ellas una descripción global adecuada. Este paso de lo local a lo global, casi nunca único, pocas veces posible y con frecuencia no obvio, es precisamente uno de los grandes retos a los que se enfrenta mucha de la matemática contemporánea.

Escher, un artista gráfico; Duchamp, un artista conceptual; Lévi-Strauss, un antropólogo; Picasso, un pintor. Cuatro ejemplos de creadores cuyas obras no pueden ser más distintas entre sí. ¿Qué hay en las matemáticas que pueda resultar de interés a todos ellos? Estructuras, andamiaje. Pólya permite a Escher identificar la estructura que subyace a los recubrimientos de un plano mediante losetas. Poincaré permite a Duchamp estructurar su trabajo al margen de las tradiciones artísticas convencionales. Weil permite a Lévi-Strauss identificar las reglas que rigen ciertas relaciones de parentesco, y la geometría permite a Picasso construir estructuras adecuadas sobre las que encolar detalles locales para construir imágenes globales coherentes. A su vez, todos ellos, y muchos más, nos permiten a los profesores de Matemáticas encender de vez en cuando en el aula o la sala de conferencias un interruptor que lleve luz, y con ella la posibilidad de ver las matemáticas contemporáneas, a nuestros alumnos.

(1)L. Henderson: The Fourth Dimension and Non-Euclidean Geometry in Modern Art. Princeton University Press, 1983.
(2)L. Henderson: Duchamp in Context: Science and Technology in the Large Glass and Related Works. Princeton University Press, 1988.
(3)C. Lévi-Strauss: Myth and Meaning. University of Toronto Press, 1978.
(4)H. Poincaré: Ciencia y método, 1908. Edición en castellano de Espasa Calpe (Colección Austral), Buenos Aires, 1944.
(5)G. Pólya: "Über die Analogie der Krystallsymmetrie der Ebene" ("Sobre la analogía de la simetría cristalina en el plano"), en Zeitshrift für Kristallographie (Revista de Cristalografía), 1924.
(6)R. Roland Shearer: "Did Poincaré Point the Way to Twentieth Century Art?", en The Sciences, marzo-abril de 1997.
(7)A. Weil, A.: The Apprenticeship of a Mathematician. Birkhäuser, 1992.
(8)A. Weil, A.: "Sur l'ètude algébrique de certain types de lois de mariage" ("Sobre el estudio algebraico de ciertos tipos de reglas de matrimonios"), en Œuvres Scientifiques/Collected Papers. Springer-Verlag, 1980